2.5 The Ideal Gas¶
https://www.youtube.com/watch?v=3j84j1PYddM&list=PLMcpDl1Pr-vjXYLBoIULvlWGlcBNu8Fod&index=20
Introduction¶
In this section, we’re going to rely on Quantum Mechanics to calculate the multiplicity of an ideal gas. We’ll start with one monatomic molecule, then 2, and then N. We’ll need to calculate the surface area of a hypersphere in 3N dimensions, where N could be near Avogadro’s number. We’ll note similarities between this and the Einstein Solid we already visited, and then make some observations about what happens when two ideal gases interact through an exchange of energy, volume, and particles. Finally, I’ll wrap up talking about how unlikely it is to find anything but the most likely cases.
The point is to show that any two systems, when brought into thermal contact, will move toward a very definite state, with very little distribution, given even a small number of degrees of freedom and such. This sets us up for a general discussion about this universal observation, which we will call entropy and the 2nd Law of Thermodynamics.
Background¶
Last section we dealt with “very big numbers”.
Before that we learned how to count the states in Einstein Solids and Paramagnets.
Multiplicity of a Monatomic Ideal Gas¶
1 Monatomic Particle¶
How can we count the number of states in an ideal gas?
Let’s start with a single molecule, something like helium, which is monatomic. We use a monatomic molecule because we don’t want to consider things like rotation and vibration.
Given one molecule of monatomic gas, it should be fairly obvious how to go to 2 or more molecules. We can add in vibration and rotation for more complex molecules later on as well.
We consider:
Total kinetic energy

Contained inside of a volume
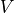
We need to know how many possible microstates can exist for the above
macrostate 
We assume:
If we double the volume, there should be twice as many microstates. Thus,
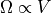
Now, when it comes to the energy, we’re going to consider what should be a new idea: momentum space. That is, if we consider that space is just a collection of possible vectors, and we consider momentum to be a vector, then we should be able to describe all the possible momentum vectors in a space. Momentum comes in 3-vectors, one for each dimension, so the momentum space would also be 3-vectors, but the length will not be distance: it will be units of mass length per time.
If we have a single molecule, and all of the internal energy must be stored as kinetic energy (since its monatomic) and all of the kinetic energy will appear as momentum, then we can think of the possible momentums (momenta?) as being the surface of a sphere in momentum space. That is:
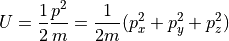
All possible combinations that satisfy the above are valid, so the total
energy describes the surface of a sphere in momentum space. The radius of that
sphere is simply 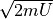 .
.
So we have that 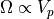 , where
, where 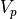 is a volume in
momentum space. (He says that the surface area can be multiplied by a small
volume. We won’t quibble over areas and volumes.)
is a volume in
momentum space. (He says that the surface area can be multiplied by a small
volume. We won’t quibble over areas and volumes.)
So, we have, in total:
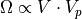
At this point, if you are thinking classically, you are probably saying to yourself that none of this matters, since there are infinite positions inside of a volume (or on the surface of a sphere, or whatever) and so we have an infinite number of possibilities.
This is where Quantum Mechanics saves the day. If we consider things from the
Quantum Mechanics perspective, then there most definitely is some countable
number of possible positions and possible momentums, and so we do not have an
infinite  . It may be very, very large, but we already know how
to deal with those sorts of numbers.
. It may be very, very large, but we already know how
to deal with those sorts of numbers.
He provides a brief overview of Quantum Mechanics in Appendix A. I don’t plan on making a video on that at this time, but it should be good review, and should get you prepped on what you need to know to understand the following.
At this point, what we need to do is decide how accurate we want to be in our measurements. Let’s say we want to cut up our volume into small slices, and then detect whether the particle is in one of those smaller volumes. Depending on how small we cut up the volume, we’re going to see a dependence on how accurate we’ll be in measuring the momentum as well.
Invoking the Heisenberg uncertainty principle, we know that there is a limit to how well-defined the position and momentum can be. In one dimension:
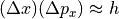
where:
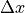 is the statistical spread in the
is the statistical spread in the 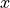 component
of the position vector
component
of the position vector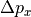 is the statistical spread in the
is the statistical spread in the
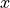 component of the momentum vector
component of the momentum vector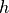 is Planck’s constant.
is Planck’s constant.
Note that Heisenberg’s uncertainty principle says that the spread in position and momentum can multiply to numbers much larger than Planck’s constant, but we’re interested in being as precise as possible. (This will give us the greatest multiplicity, after all.)
Although there are truly an infinite number of wave functions for the particle
in a box of energy  , the number of independent wave functions is
not infinite, and can be counted.
, the number of independent wave functions is
not infinite, and can be counted.
At this point, he draws a picture – Figure 2.9. This represents that when we choose a set of possible positions, we are putting some kind of constraint on the momentum space. If we were to choose wider positions, then there would be narrower momentums, and vice-versa.
From the diagram, we conclude that there are 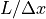 possible
positions, and
possible
positions, and 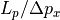 possible momentums, depending on what we
choose for
possible momentums, depending on what we
choose for 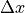 . (
. (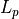 is simply the length in momentum
space.)
is simply the length in momentum
space.)
The total number of distinct combinations of these states is simply:
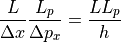
That was for the one dimensional case, so moving up to 3 dimensions we would calculate:
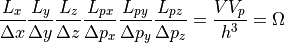
Although we don’t have any constants to multiple the above, the constants would get lost in the large numbers that are to follow. At the very least, this gives you a dimensional analysis. The units should all work out.
Note that it doesn’t matter how small we choose to divide the volumes. Or, in other words, how precise we want to be in measuring the position or momentum. Because of Heisenberg’s Uncertainty Principle, whatever we choose, we’re going to get the above possible combinations.
2 Monatomic Particles¶
This is all there is to say about the one monatomic molecule case. What happens if we have 2 molecules?
Naively, we can just multiply the one-molecule case together to get the two molecule case:
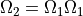
Indeed, this would give us the number of cases where the two molecules have the same energy.
However, we need to keep in mind that the energy must be shared between the two molecules. If one particle is feeling particularly energetic, the other one must be lethargic.
The total energy must thus be divided:
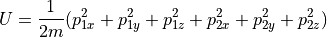
This is the surface of a sphere in 6 dimensions of momentum space, with a
radius of 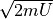 .
.
Playing with math as we did above, we’ll get to a similar conclusion:
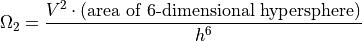
The only remaining issue is that in Quantum Mechanics, the two particles are completely indistinguishable, so we need to consider that if particle A is in such-and-such a position, and particle B is in such-and-such a position, then it is also counting as it they were reversed. Ignoring the fraction of the times the particles are in the same state, we get:
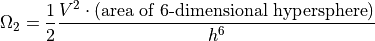
N Monatomic Particles¶
Using the same logic for  particles, we get:
particles, we get:

The 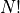 comes from the number of ways to order
comes from the number of ways to order  things.
things.
The hypersphere still has a radius of 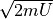 .
.
Surface Area of an N-Dimensional Hypersphere¶
In all of physics, this was the most enjoyable thing I remember. If you study math at any level, you probably wonder things like, “How many dimensions are there?” and “What is the surface area / volume of objects in those dimensions?”
In thermodynamics, we get to calculate the surface area of a sphere in dimensions proportional to the number of particles in a gas.
Although I have yet to visualize a 4-dimensional sphere (4-dimensional “cubes” are hard enough”), the math isn’t that hard, and it is in Appendix B. (I want to make a video on that at some future day! Stay tuned.)
The formula is:
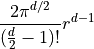
where:
 is the radius of the hypersphere.
is the radius of the hypersphere.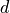 is the number of dimensions.
is the number of dimensions.
Note that 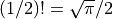 . (Yes, this does invole the gamma
function.)
. (Yes, this does invole the gamma
function.)
Final Formula¶
For our case, we have 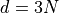 and
and 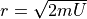 , so the
multiplicity is:
, so the
multiplicity is:
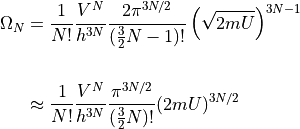
We dropped the 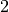 and brought in some factors because it simplifies the
formula. We’re dealing with very large numbers and it won’t affect the result.
and brought in some factors because it simplifies the
formula. We’re dealing with very large numbers and it won’t affect the result.
The formula can be broken up into parts depending on the energy and volume:
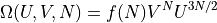
where:
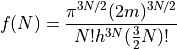
Note the similarity between the formula for the multiplicity of a monatomic
ideal gas and an einstein solid. In the einsteinian solid, the multiplicity is
related to the power of 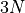 (where N is the number of particles) and
here it is
(where N is the number of particles) and
here it is 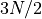 . This has to do with quadratic degrees of freedom.
. This has to do with quadratic degrees of freedom.
Interacting Ideal Gases¶
If we have two monatomic ideal gasses separated by a membrane that allows energy to pass between them, how will the energy end up being allocated? Much like our example with Einstein solids (and paramagnets), if we allow sufficient time for energy to distribute randomly, we are most likely to reach some equilibrium point. The question, as before, is where that point should be as well as how likely is it that it will deviate by that point by a certain amount. Are we to find the same result, that the distribution is extraordinarily narrow such that we can have every confidence that it will be unmeasurably near the equilibrium?
The multiplicity of the entire system is:
![\Omega_\text{total}
= \Omega_A \Omega_B
= [f(N_A)V_A^{N_A} U_A^{3N_A/2}]
[f(N_B)V_B^{N_B} U_B^{3N_B/2}]](../../_images/math/170afcb6beb8270c81168418ed100e0049f018ef.png)
Suppose we fix the number of particles to be equal on either side: 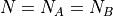 :
:
![\Omega_\text{total}
= [f(N)V_A^{N} U_A^{3N/2}]
[f(N)V_B^{N} U_B^{3N/2}]
= f(N)^2 (V_A V_B)^N (U_A U_B)^{3N/2}](../../_images/math/0bb62ef9fd6ddea1a1754ee8ccc2263d44a9864f.png)
This obviously reaches its maximum around 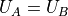 and so half the
energy will end up in one side and half in the other.
and so half the
energy will end up in one side and half in the other.
If we were to measure the width of the peak, we would find it is about
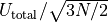 wide, which is a very, very small number.
wide, which is a very, very small number.
What if we allowed energy and volume to be exchanged? This would be like
placing the gases on either side of a chamber with a piston separating them,
allowing heat to transfer through the piston. Using the same formula as above,
if the two sides have the same number of particles, then we’d find that
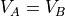 and the width of that peak is about
and the width of that peak is about
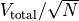 .
.
If we were to allow particles to freely travel from one side to another, which is a bit more complicated, we’d find that they would reach an equilibrium point with the highest multiplicity where the density on either side is equal, again, with a very narrow width.
Suppose we wanted to calculate something weird, like all the particles being
in one side of the two chambers. We can calculate the multiplicity of that
macrostate, and then compare it with the most likely macrostate. In which
case, we’d find that there is a 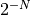 probability, which is so
unlikely when N is 100 that you can check the state
trillions of times a second for the age of the universe and perhaps see it
only once. For Avogradro’s number, it’s simply ridiculous.
probability, which is so
unlikely when N is 100 that you can check the state
trillions of times a second for the age of the universe and perhaps see it
only once. For Avogradro’s number, it’s simply ridiculous.
Problem 2.27¶
Calculate the likelihood that only 99% of the molecules are on one side of the chamber.

